[Hinton NN] Lecture 2 - The Perceptron learning procedure

NN 아키텍쳐의 주요 타입

Feed-Forwad NN

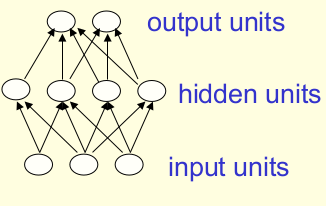
• 가장 보편적인 타입이다.
  • 첫 레이어가 input 레이어, 마지막 레이어가 output 레이어다.
  • hidden 레이어가 한 개 이상일 때 “deep” NN이라고 부른다.
• They compute a series of transformations that change the similarities between cases.
• 각 뉴런의 activities는 아랫 단계의 레이어의 activities의 non-linear 함수다.

Recurrent networks

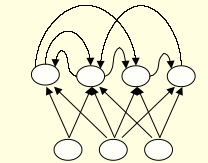
• Directed Cycle을 가지고 있다.
• 복잡한 로직을 수행할 수 있지만 학습을 더 어렵게 만들기도 한다.
  • 최근에 recurrent network를 효율적으로 학습할 방법이 많이 연구되고 있다.
• 생물학적으로 현실적이다.(Biologically Realistic)

Recurrent neural networks for modeling sequences

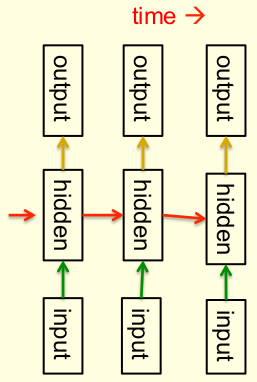
• 순차적인 데이터(Sequential Data)를 모델링 하는데 가장 자연스러운 방법이다.
  • 타임 슬라이스당 하나의 hidden 레이어를 도는 매우 깊은(deep) 네트워크와 동일하다.
  • 모든 타임 슬라이스마다 같은 weight를 사용하고 매 타임 슬라이스마다 input을 받는다.
• 장기간 숨겨진 상태에 대한 정보를 저장할 수 있다.
  • 이러한 능력을 끌어내도록 학습시키는 것은 매우 어렵다.

    Symmetrically connected networks with hidden units

• Recurrent Network와 비슷하지만 연결이 대칭적(symmetric)이라는 점이 다르며 두 방향의 연결 모두 같은 weight를 가지고 있다.
• hidden 레이어가 없으면 “Hopfield nets”로 불리고, hidden레이어가 있으면 “Boltzmann machines”으로 불린다.
  • Recurrent Network보다는 강력하지 않다.
  • 학습 알고리즘이 간단하다.

The first generation of neural networks

Binary threshold neurons (decision units)

$$z = b+\sum_i x_i w_i$$ $$y = \begin{cases} 1 & \text{if $ z \geq 0 $}.\\ 0 & \text{otherwise}. \end{cases}$$

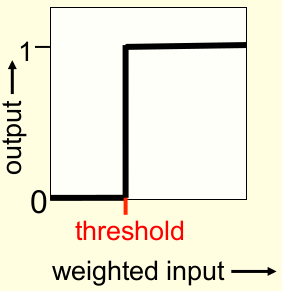
• 우선 다른 뉴런에서 온 input의 weighted sum을 계산하고 bias를 더한다.
• 계산한 값이 0이 넘으면 1을 output으로 내보낸다.

Bias를 다른 weight가 사용하는 알고리즘으로 학습시키는 방법

Bias를 weight처럼 생각하고 bias에 해당하는 input으로 1을 넣는다.

퍼셉트론 수렴 과정 - binary output 뉴런 학습시키기

1. input에 1 값을 가지는 column을 추가한다. “bias” weight는 -threshold다.
2. 학습할 데이터 중 하나를 선택한다. 어떤 방법이든 상관없으며 최종적으로 모든 데이터를 선택할 수 있기만 하면 된다.
   • 만약 output unit이 맞으면, weight를 그대로 둔다.
   • 만약 output unit이 0이고 틀렸으면, weight_vector += input_vector
   • 만약 output unit이 1이고 틀렸으면, weight_vector -= input_vector

Weight space

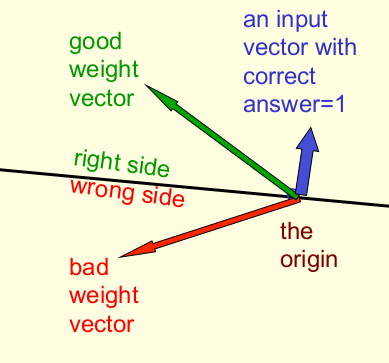
• 각각의 학습 데이터(training case)는 하나의 평면을 정의한다.(위 그림에서 검은 선)
• 학습 데이터에 의해 정의된 평면은 원점을 지나며 input 벡터에 직교(perpendicular)한다.
• 평면의 한쪽 면은 틀린 output을 가진다.

가능한 솔루션의 원뿔(The cone of feasible solutions)

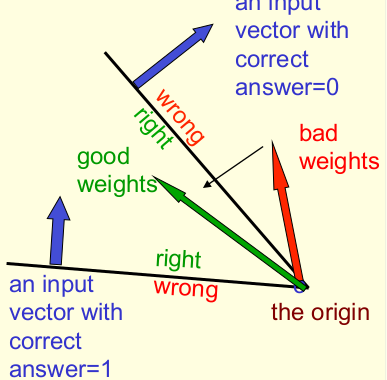
• 모든 학습 데이터가 맞도록 하기 위해서 모든 평면들의 맞는 부분의 점을 찾아야 한다.
  • 위 그림에서 두 검은 선은 두 학습데이터가 만들어낸 평면을 의미하고 그 사이가 good weight를 가지는 부분이다. 학습은 good weight인 부분의 한 점을 찾는 과정이라고 볼 수 있다.
  • 찾고자 하는 점이 존재하지 않을 수도 있다.
• 만약에 모든 학습 데이터를 만족하는 점이 존재하면 그 점들은 hyper-cone의 정상에 있다.
  • 두 good weight 벡터의 평균은 항상 good weight 벡터다.
  • 문제가 convex하다는 것을 의미한다.

Why the learning procedure works (first attempt)

Informal sketch of proof of convergence

The limitations of Perceptrons

A geometric view of what binary threshold neurons cannot do

Learning with hidden units

• adpatvie하고 non-linear한 hidden unit이 필요하다.
  • 마지막 레이어 뿐 아니라 모든 weight를 adpat할 효율적인 방법이 필요하다.